Detect Cycles in Directed Graphs

Rate this post

Programmers always face difficulty in implementing “Detect Cycles in Directed Graphs” and it becomes even harder to code during interviews. In this post, we will break down the problem and understand how to implement it simply.

Graphs, a fundamental data structure in computer science, model various real-world scenarios, from social networks to transportation systems. Among the many types of graphs, directed graphs, or digraphs, are particularly intriguing. They represent relationships with direction, making them suitable for modeling processes like dependency, causality, and flow.

One essential task in graph analysis is detecting cycles within directed graphs. Cycles, or loops, are paths within a graph where you can start and finish at the same node, moving through other nodes in between. Detecting cycles is valuable for uncovering dependencies, preventing deadlocks, and optimizing algorithms. In this comprehensive exploration, we’ll delve into the world of directed graphs, cycle detection, and their practical applications.

Table of Contents

Understanding Directed Graphs

Before we venture into cycle detection, let’s build a strong foundation by understanding what directed graphs are and how they work. A directed graph often denoted as “DAG” (Directed Acyclic Graph) when it lacks cycles, consists of nodes (vertices) and directed edges connecting them. Each edge has a direction, indicating the flow or relationship from one node to another.

Directed graphs are versatile tools for modeling a wide range of scenarios. Consider a few examples:

Dependency Graphs: In software development, directed graphs can represent dependencies between components or libraries, ensuring that one piece is built or executed before another.
Flow Networks: Directed graphs are ideal for modeling transportation networks, like road systems, airlines, or data flow in computer networks.
Causality and Event Sequencing: Events can be linked in a directed graph to depict causal relationships or chronological sequences.
Hierarchies: Organizational structures, taxonomies, or classification systems can be represented using directed graphs.

Now that we’ve established the importance and versatility of directed graphs let’s turn our attention to the central theme: finding cycles within these graphs.

The Challenge of Detecting Cycles in Directed Graphs

Cycles within directed graphs pose intriguing challenges. In many scenarios, detecting and understanding these cycles is vital. Consider the following examples:

Dependency Resolution: In a software project, you want to ensure that there are no circular dependencies that could lead to build failures or runtime errors. Detecting cycles in the dependency graph helps you prevent these issues.
Resource Allocation: In resource allocation problems, cycles might indicate inefficient utilization, where resources flow through a loop instead of reaching their destination.
Deadlock Avoidance: In concurrent systems, cycles in resource allocation graphs can result in deadlocks. Identifying and resolving these cycles is crucial for ensuring system stability.
Optimization: In optimization problems, understanding cycles can reveal opportunities for improving processes and reducing resource wastage.

To address these challenges, various algorithms have been developed for cycle detection in directed graphs. Let’s explore some of these algorithms and their applications.

Common Algorithms to Detect Cycles in Directed Graphs

1. Depth-First Search (DFS)

DFS is a fundamental algorithm for traversing graphs and is often used for cycle detection. The key idea is to start at a node and explore as far as possible along each branch before backtracking. When the algorithm encounters a node that has already been visited, it has found a back edge, indicating the presence of a cycle.

The complexity of DFS is O(V + E), where V is the number of vertices and E is the number of edges. While it’s efficient for most practical purposes, it can be slower in the presence of large graphs.

2. Tarjan’s Algorithm

Tarjan’s algorithm, a more advanced approach, utilizes depth-first search for cycle detection. It assigns a unique identifier (called a low-link value) to each node based on its traversal order and the nodes it can reach. If a node’s low-link value matches its identifier, it is part of a strongly connected component (SCC) and contributes to a cycle.

This algorithm has a time complexity of O(V + E) and is particularly efficient for detecting strongly connected components in directed graphs.

3. Johnson’s Algorithm

Johnson’s algorithm combines both DFS and Tarjan’s algorithm to efficiently detect cycles in directed graphs. It first runs Tarjan’s algorithm to identify SCCs, which are subgraphs containing nodes with cyclic dependencies. Then, it examines these SCCs to pinpoint the specific cycles.

Johnson’s algorithm has a time complexity of O(V^2 + VE) and is efficient for practical use. It’s particularly useful in scenarios where the directed graph is known to be sparse.

Example: Detecting Cycles in a Software Dependency Graph Using DFS

Suppose you are a software engineer working on a complex project that involves multiple code modules and libraries with dependencies. To ensure the project builds and runs smoothly, you need to detect any circular dependencies in the software’s dependency graph.

Directed Graph Representation:

Consider a simplified directed graph representing the software project’s dependency relationships. The nodes represent code modules or libraries, and the directed edges represent dependencies between them.

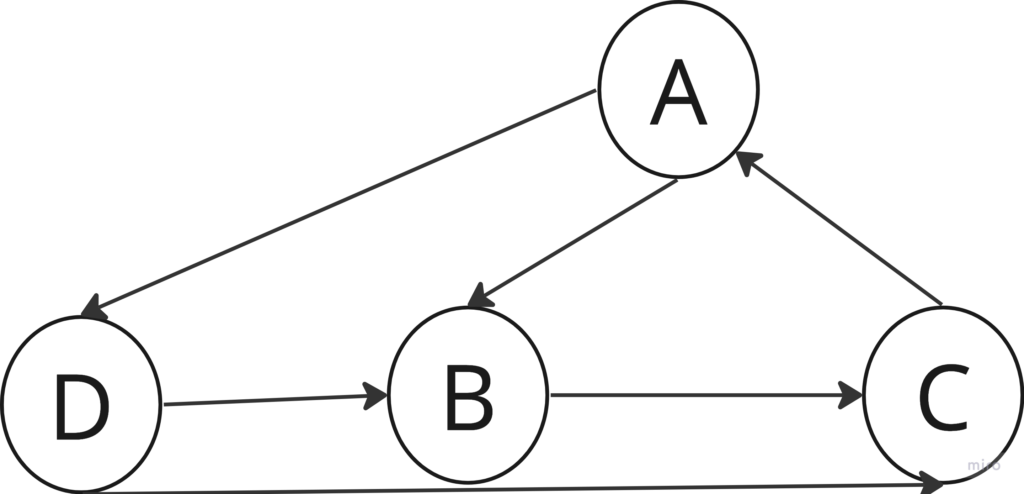
In this graph:

A depends on B and D.
B depends on C.
C depends on A.
D depends on B and C.

Detecting Cycles with Depth-First Search (DFS):

Let’s apply the Depth-First Search (DFS) algorithm to identify cycles in this graph. We’ll start the DFS from each node and mark visited nodes. If we encounter a visited node during the traversal, it indicates a cycle.

Cycle Detection Process:

Begin DFS from node A.
- A → B (visited)
  - B → C (visited)
    - C → A (visited)
      - A is visited, indicating a cycle: A → B → C → A.
Restart DFS from node B.
- B → C (visited)
  - C → A (visited)
    - A is visited, indicating a cycle: B → C → A.
Restart DFS from node C.
- C → A (visited)
  - A → B (visited)
    - B is visited, indicating a cycle: C → A → B.
Restart DFS from node D.
- D → B (visited)
  - B → C (visited)
    - C → A (visited)
      - A is visited, indicating a cycle: D → B → C → A.

Detected Cycles:

The DFS algorithm has successfully identified the following cycles in the directed graph:

A → B → C → A
B → C → A
C → A → B
D → B → C → A

Here’s a Go code example for detecting cycles in a directed graph using the Depth-First Search (DFS) algorithm:

package main

import "fmt"

type Graph struct {
	nodes     []int
	adjacency map[int][]int
}

func NewGraph() *Graph {
	return &Graph{
		adjacency: make(map[int][]int),
	}
}

func (g *Graph) addEdge(u, v int) {
	g.adjacency[u] = append(g.adjacency[u], v)
}

func hasCycle(g *Graph, node int, visited, recursionStack map[int]bool) bool {
	visited[node] = true
	recursionStack[node] = true

	for _, neighbor := range g.adjacency[node] {
		if !visited[neighbor] {
			if hasCycle(g, neighbor, visited, recursionStack) {
				return true
			}
		} else if recursionStack[neighbor] {
			return true
		}
	}

	recursionStack[node] = false
	return false
}

func detectCycle(g *Graph) bool {
	visited := make(map[int]bool)
	recursionStack := make(map[int]bool)

	for _, node := range g.nodes {
		if !visited[node] {
			if hasCycle(g, node, visited, recursionStack) {
				return true
			}
		}
	}
	return false
}

func main() {
	graph := NewGraph()
	graph.nodes = []int{0, 1, 2, 3}

	// Add directed edges to the graph
	graph.addEdge(0, 1)
	graph.addEdge(1, 2)
	graph.addEdge(2, 0)
	graph.addEdge(3, 1)

	if detectCycle(graph) {
		fmt.Println("The graph contains cycles.")
	} else {
		fmt.Println("The graph is acyclic.")
	}
}

In this Go code, we define a Graph struct to represent the directed graph, and we implement the detectCycle function that utilizes Depth-First Search (DFS) to check for cycles in the graph. The hasCycle function is a recursive helper function that performs the DFS traversal and identifies cycles.

The code starts by creating a directed graph, adding edges to it, and then calling detectCycle to check for cycles. If cycles are detected, it prints that the graph contains cycles; otherwise, it indicates that the graph is acyclic.

Practical Applications of detecting cycles in the directed graph

Understanding cycle detection algorithms in directed graphs has practical applications across various domains. Let’s delve into some real-world scenarios where these algorithms are indispensable.

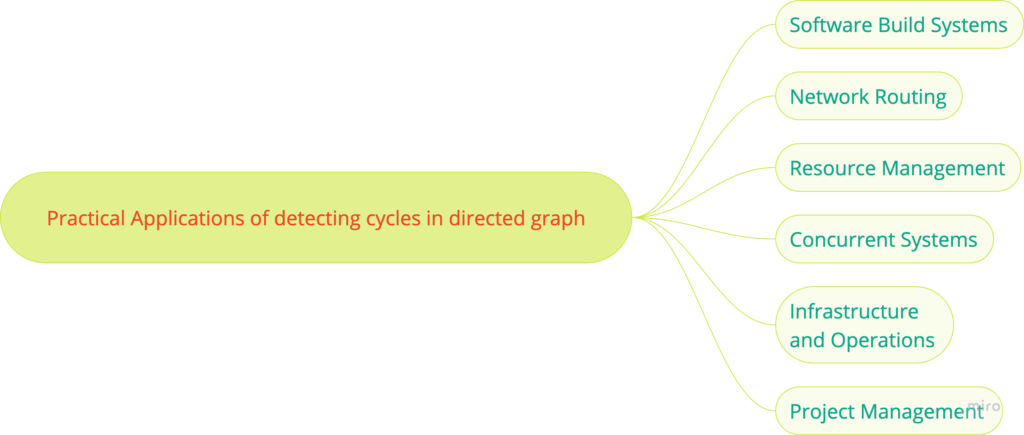
1. Software Build Systems

In software development, managing dependencies is crucial to building and running applications. A directed graph can represent the dependency relationships between code modules, libraries, or components. Detecting cycles in this graph ensures that no circular dependencies exist, preventing build errors and runtime issues.

2. Network Routing

Computer networks, especially in the context of routing, involve complex interactions between devices and data flows. Detecting cycles in network topologies helps avoid routing loops and ensures efficient data transmission.

3. Resource Management

In resource allocation problems, such as task scheduling or optimizing the use of resources in cloud computing, detecting cycles is essential. It helps identify and resolve inefficiencies, ensuring that resources are used effectively without unnecessary wastage. This is particularly critical in cloud computing, where resource allocation can have significant cost implications.

4. Concurrent Systems

Concurrent systems often involve resource allocation and synchronization. Detecting cycles in the dependency graphs of resource allocation can help avoid deadlocks, a scenario where processes are stuck waiting for each other to release resources. By preventing deadlocks, systems can maintain high availability and reliability.

5. Infrastructure and Operations

In infrastructure management, understanding the dependencies and relationships between various components is vital for ensuring system stability and efficient operations. Detecting cycles in infrastructure dependency graphs allows for proactive issue resolution and optimization.

6. Project Management

Project management tools often employ directed graphs to model tasks, dependencies, and project timelines. Detecting cycles in these graphs helps identify task dependencies that may lead to project delays or bottlenecks, enabling project managers to make informed decisions and adjust schedules accordingly.

5 FAQs on Cycle Detection in Golang

1. What is cycle detection in GoLang?

Cycle detection involves identifying situations where data structures like graphs or linked lists have circular references, creating loops where traversing elements lead back to the starting point. This can cause infinite loops and unexpected behavior in your program.

2. How do you detect cycles in GoLang?

There are various methods for cycle detection, depending on the data structure:

Graphs: Depth-First Search (DFS) with a visited set to track nodes already visited. If you revisit a node encountered earlier, a cycle exists.
Linked lists: Floyd’s Cycle Finding Algorithm uses two pointers moving at different speeds. If they meet, a cycle is present.
Recursive structures: Utilize a set to keep track of encountered objects. If a function encounters an object already in the set, a cycle exists.

3. What are some popular libraries or tools for cycle detection in GoLang?

Graphs: The “graph” package offers DFS functionality for cycle detection.
Linked lists: Implementations like “singlelinkedlist” or “doublylinkedlist” might have built-in methods for cycle detection.
Other structures: Utilize generic approaches like marking visited objects in a map using reflection libraries.

4. What are the potential challenges of cycle detection in GoLang?

Performance: Extensive graph traversals in complex structures can impact performance.
False positives: Depending on the algorithm and data structure, you might encounter situations where the “cycle” doesn’t represent a problem but reflects expected data relationships.
Memory usage: Tracking visited elements or building large sets can increase memory usage in certain scenarios.

5. When should you consider using cycle detection in GoLang?

Implement cycle detection when:

Working with graphs representing relationships that must not form loops (e.g., dependency graphs).
Validating user-provided data structures that could contain cycles unintentionally.
Debugging or analyzing complex data structures for potential infinite loops.

Conclusion

In this exploration of detecting cycles in directed graphs, we’ve delved into the fundamental concept of identifying cycles in complex networks. The ability to uncover cyclic dependencies within directed graphs is invaluable, with practical applications spanning various domains, from software engineering to network management and resource allocation.

We began by understanding directed graphs, their representation, and their diverse applications. Directed graphs are a versatile tool for modeling relationships with direction, making them suitable for scenarios involving dependencies, causality, and flow.

The challenge of cycles within directed graphs was then addressed. We examined why detecting cycles is crucial, especially in scenarios like software build systems, network routing, resource management, concurrent systems, and project management.

To tackle this challenge, we explored common algorithms for cycle detection, including Depth-First Search (DFS), Tarjan’s Algorithm, and Johnson’s Algorithm. These algorithms play a vital role in efficiently identifying cycles within directed graphs, each with its strengths and use cases.

Practical applications of cycle detection were highlighted, showcasing how this knowledge is put into action in real-world scenarios. From ensuring clean software builds and efficient network routing to optimizing resource allocation and avoiding deadlocks, cycle detection is the cornerstone of reliability and efficiency in complex systems.

In conclusion, the ability to detect cycles in directed graphs is a fundamental skill with a broad spectrum of applications. It empowers professionals in various fields to make informed decisions, prevent issues, and optimize processes. As technology continues to evolve, the role of directed graphs and cycle detection algorithms becomes increasingly critical, making this knowledge a valuable asset in computer science and engineering.

Whether you are a software developer, a network engineer, or a project manager, mastering cycle detection in directed graphs is a key step toward efficiency and success in your field.

Cycle Detection in Directed Graphs in Golang with an Easy Approach in 2024